Pavement Thickness Calculator
Fast plugin-free formula rendering using KaTeX auto-render. :contentReference[oaicite:2]{index=2}
AASHTO 1993 Flexible Pavement (Solve for SN)
Design equation:
\[ \log_{10}(W_{18}) = Z_R S_o + 9.36\log_{10}(SN+1) - 0.20 + \frac{\log_{10}\left(\frac{\Delta PSI}{4.2-1.5}\right)}{0.4 + \frac{1094}{(SN+1)^{5.19}}} + 2.32\log_{10}(M_R) - 8.07 \]
We solve for \(SN\) numerically, then show a single-layer equivalent thickness: \(D = \frac{SN}{a_1 m_1}\).
CBR Thickness (Simplified Empirical)
Formula: \(T = k\left(\frac{P}{CBR}\right)^n\)
Westergaard Rigid Pavement (Load Stress Only)
\[ l = \left(\frac{E h^3}{12K(1-\nu^2)}\right)^{1/4} \]
We iterate \(h\) until maximum stress is below allowable stress.
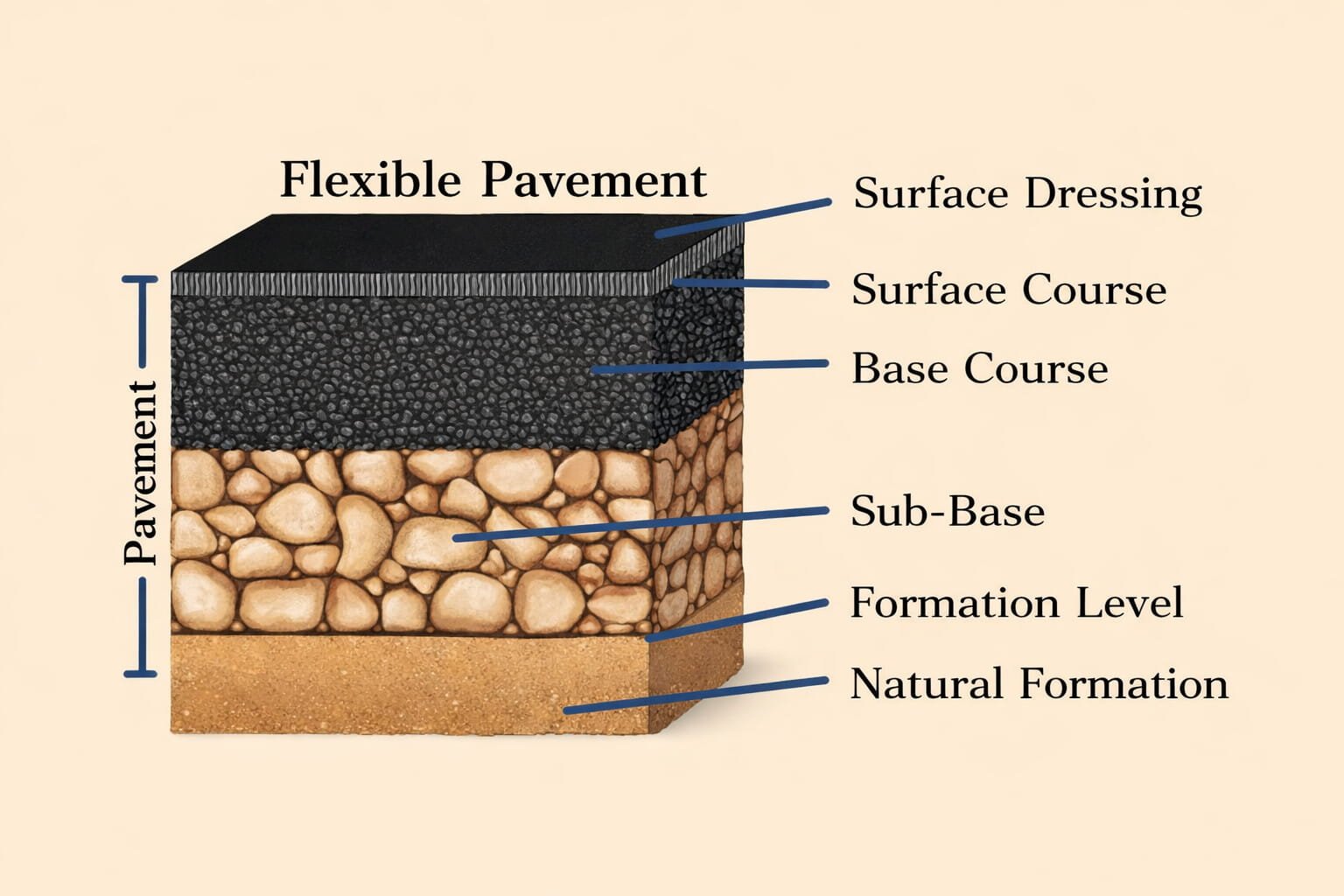
Common Pavement Terms and Their Descriptions
Here’s a table summarizing the different names and descriptions of pavement:
| Term | Description |
|---|---|
| Pavement | General term for any surface designed for vehicles or pedestrians, typically hard-surfaced. |
| Road Surface | A broad term for the topmost layer of a road designed for vehicle travel. |
| Carriageway | Commonly used in British English, referring to the portion of the road where vehicles travel. |
| Highway Surface | Used for larger roads, especially in North America, such as highways or major arterials. |
| Asphalt | Often used interchangeably with pavement, referring to a bitumen-based road surface. |
| Tarmac | Originally referred to tar-bound macadam roads; now often used to mean asphalt, especially in the UK. |
| Bitumen Road | Refers specifically to roads surfaced with bitumen, a binding agent in asphalt. |
| Macadam | An older term for roads constructed with layers of crushed stone, often bound with tar or bitumen. |
| Concrete Road | Refers to roads with a surface made of concrete rather than asphalt. |
| Flexible Pavement | Pavements designed to flex under load, typically using asphalt or bituminous materials. |
| Rigid Pavement | Pavements made from concrete that do not flex under load, unlike flexible pavement. |
| Street Surface | Common in urban areas, referring to the road surface designed for vehicles and sometimes pedestrians. |
| Footpath / Sidewalk | A paved path for pedestrian traffic, usually alongside a road. (UK: Footpath, US: Sidewalk) |
| Blacktop | A term used in the US to refer to asphalt roads, typically with a dark appearance. |
| Driveway | A smaller paved surface leading to private properties, commonly found near homes. |
| Gravel Road | An unpaved road made of loose gravel, commonly found in rural areas. |
| Cobblestone Road | An older type of road surface made of small stones or bricks, often found in historical areas. |
| Seal Coat | A thin layer of asphalt or bituminous material applied over a road surface to refresh or protect it. |
Pavement Thickness Design: A Comprehensive Guide
Pavement thickness design is a critical aspect of road and highway engineering. It determines the capacity of the pavement structure to withstand traffic loads over its design life without experiencing significant damage or failure. Engineers use different methods to calculate the thickness required for both flexible pavements (such as asphalt) and rigid pavements (such as concrete). This article discusses three popular pavement design methods: AASHTO, CBR, and Westergaard, including the formulas used in each method and a guide on when to use them.
1. AASHTO Pavement Design Method
The AASHTO (American Association of State Highway and Transportation Officials) method is widely used in the USA for both flexible and rigid pavements. This method is based on empirical data collected from field tests and considers traffic loads, subgrade conditions, and environmental factors.
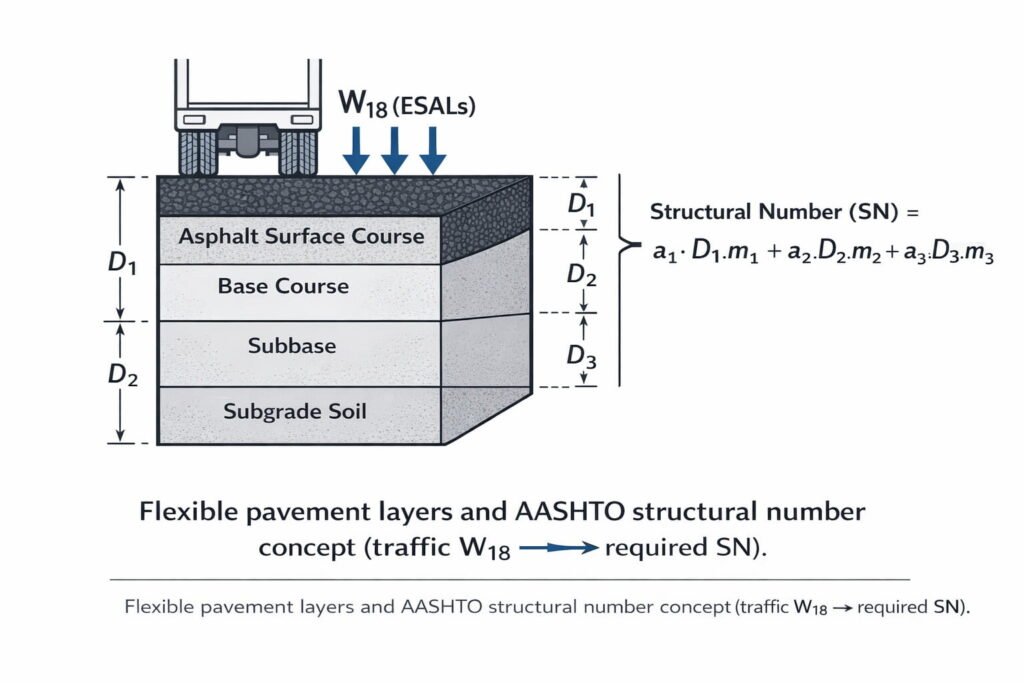
AASHTO 1993 Formula for Flexible Pavements
Design Equation
Abbreviations / Symbols
- \(W_{18}\): 18-kip Equivalent Single Axle Loads (ESALs) — design traffic in 18-kip equivalents
- ESALs: Equivalent Single Axle Loads
- \(Z_R\): Standard normal deviate for reliability \(R\)
- \(R\): Reliability (%) — probability of satisfactory performance
- \(S_o\): Overall standard deviation (model/traffic variability)
- \(SN\): Structural Number (overall structural capacity index)
- \(\Delta PSI\): Change in serviceability index \((PSI_{initial} – PSI_{terminal})\)
- PSI: Present Serviceability Index
- \(M_R\): Resilient Modulus of subgrade (commonly psi or MPa)
- \(\log_{10}(\cdot)\): Base-10 logarithm
When to Use:
The AASHTO method is best suited for roads and highways with high traffic volumes and varying environmental conditions, making it highly adaptable. The structural number (SN) can be used to define the thickness of individual pavement layers (surface, base, and sub-base).
2. CBR Method for Flexible Pavements
The CBR (California Bearing Ratio) method is commonly used in India, the UK, and many other regions. It is particularly suited for flexible pavements and is relatively simpler than AASHTO, making it ideal for smaller projects or where detailed data is unavailable.
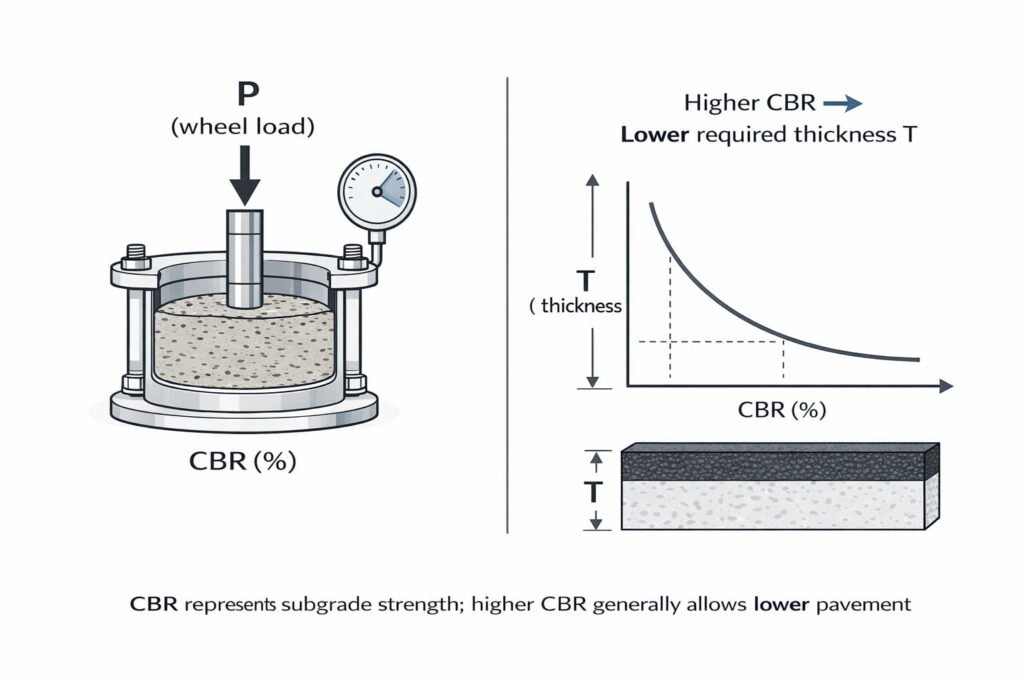
CBR Method for Flexible Pavements
General Empirical Thickness Form
This is a commonly used empirical representation. In many standards, CBR-based design is often done using design charts/catalogs (traffic class + CBR) rather than one single equation.
Abbreviations / Symbols
- \(T\): Total pavement thickness (commonly mm)
- \(P\): Wheel load (use consistent units with your chosen \(k\))
- \(CBR\): California Bearing Ratio of subgrade (%)
- \(k\): Empirical constant (depends on method/units/standard calibration)
- \(n\): Empirical exponent (often taken around 0.3–0.5 in simplified use)
Tip: If you publish this publicly, mention the standard/source you’re following (e.g., a national design catalog), because \(k\) and \(n\) are not universal.
When to Use:
The CBR method is suitable for rural roads, access roads, and low-traffic areas where simplicity and adaptability are key. It’s widely accepted by organizations like the Indian Road Congress (IRC) and the British Standards Institution (BSI).
3. Westergaard Method for Rigid Pavements
For rigid pavements, especially concrete roads, the Westergaard method is widely used. It is based on the theory of elastic plates and considers factors like slab thickness, load, subgrade support, and critical stress levels.
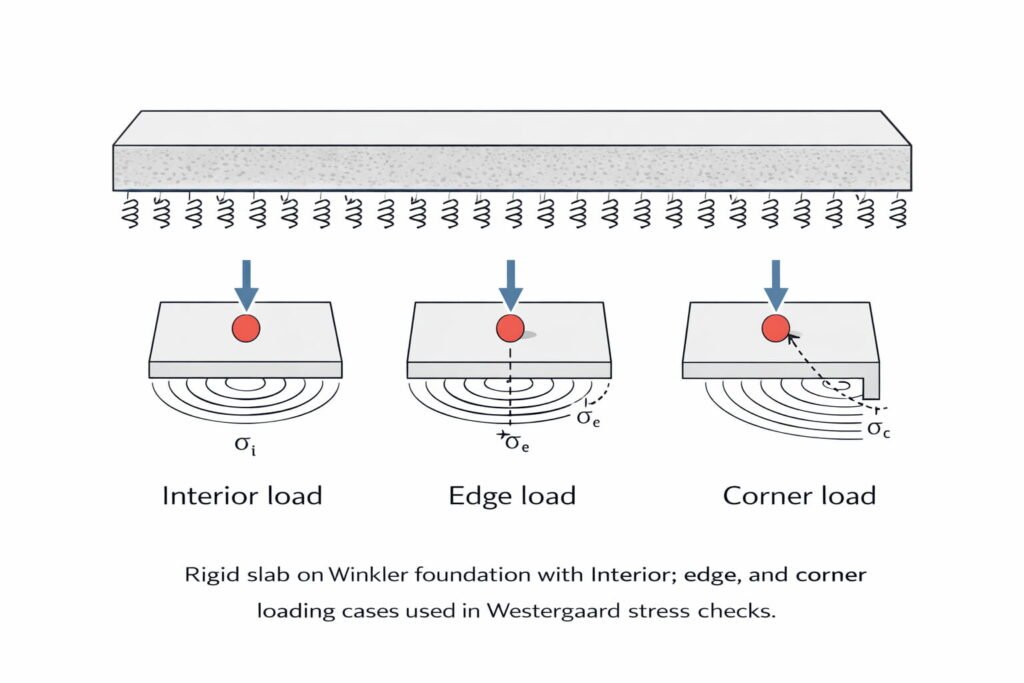
Westergaard Method for Rigid Pavements
Radius of Relative Stiffness
Load Stress (Common Westergaard Forms)
For a circular contact area (radius \(a\)) and slab thickness \(h\), common tensile stress equations are:
Abbreviations / Symbols
- \(P\): Wheel load (use consistent units)
- \(a\): Radius of circular contact area
- \(h\): Slab thickness
- \(E\): Modulus of elasticity of concrete
- \(\nu\): Poisson’s ratio of concrete
- \(k\): Modulus of subgrade reaction
- \(l\): Radius of relative stiffness
- \(\sigma_i\): Interior tensile stress
- \(\sigma_e\): Edge tensile stress
- \(\sigma_c\): Corner tensile stress
- \(\log_{10}(\cdot)\): Base-10 logarithm
When to Use:
The Westergaard method is ideal for heavy-duty roads, highways, and industrial pavements that need to withstand large, concentrated loads, such as trucks or equipment.
Why Use a Pavement Thickness Calculator?
Accurately calculating pavement thickness is crucial for ensuring the longevity and performance of roadways and pavements. Overestimating thickness can result in unnecessary costs, while underestimating can lead to pavement failures, potholes, and frequent maintenance.
Key Pavement Terms
- Subgrade: The native soil on which the pavement is built. It’s important to assess the subgrade’s load-bearing capacity when designing the pavement thickness.
- Base Course: The layer between the subgrade and surface course, usually made of aggregates to distribute the load.
- Surface Course: The top layer of the pavement, often made of asphalt or concrete, designed to bear traffic loads and resist wear.
- ESAL (Equivalent Single Axle Load): A measure of the cumulative effect of traffic loading over time, often based on a standard 18,000 lb (80 kN) axle load.
- Modulus of Elasticity (E): A measure of a material’s stiffness, used in the design of rigid pavements.
Factors That Affect Pavement Thickness
Several factors impact the thickness of pavement required for a project. These include:
- Traffic volume and vehicle weight: Heavier vehicles like trucks exert more pressure on the pavement.
- Soil properties: Poor subgrade conditions may demand thicker pavement layers to provide stability.
- Pavement materials: Different materials, such as concrete and asphalt, have different strengths and require different thicknesses to perform optimally.
- Environmental conditions: Freezing, thawing, and drainage can influence pavement performance and may require adjustments to thickness.
Frequently Asked Questions (FAQ)
1. What is the difference between flexible and rigid pavements?
Flexible pavements are made from materials like asphalt that flex under loads, distributing stresses over a larger area. Rigid pavements, typically made of concrete, are stiffer and distribute loads over a smaller area with less deflection.
2. What is the purpose of the subgrade in pavement design?
The subgrade acts as the foundation for the pavement structure. Its stability and load-bearing capacity are critical to the longevity and performance of the pavement. Poor subgrade conditions can lead to premature pavement failure.
3. How do traffic loads affect pavement design?
Pavement thickness is directly influenced by traffic loads. Roads subjected to heavier traffic loads or higher traffic volumes require thicker pavement layers to withstand wear and tear and prevent fatigue cracking.
4. Why is the modulus of elasticity important for rigid pavements?
The modulus of elasticity (E) is a measure of the stiffness of the concrete slab. It influences how the pavement will distribute loads and resist bending under heavy loads, making it a crucial factor in the design of rigid pavements.
5. What role does the drainage coefficient play in pavement design?
Drainage affects the longevity of pavements, especially flexible pavements. A proper drainage coefficient ensures that water does not accumulate beneath the pavement layers, which can weaken the subgrade and cause premature pavement failure.
Greate tool thank you so much